

In this article, we have listed and explained the real-life applications of 24 Different Data Structures ranging from common ones like Array, Linked List to Geometric Data Structures like R-Tree to Probabilistic Data Structures like LogLog.
Table of contents
The field of computer science started emerging in the mid-20th century. As it started to grow the need to organize and store data, in a way that made it easier to access and manipulate also emerged. Then the scientists began to adapt the mathematical concepts of data organization to meet the needs of the computers, which gave birth to the field of Data Structures.
In the early days the data structures developed were relatively simple and included things like arrays and linked lists, but over
time as the computers became more powerful, new algorithms and techniques were developed, the field of data structures grew to
encompass a wide variety of more complex data structures such as trees, graphs and other advanced structures.
The study of data structures and algorithms is considered as a fundamental part of computer science, and it continues to evolve day by day. As our computer technology advances, new methods are developed and new areas of applications are emerging. Today data structure and algorithms are important aspects in computer science and are used in almost all areas of computer science including operating systems, databases, compilers, artificial intelligence, and more.
Data structures are classified into linear data structure and non-linear data structure.
Now lets get to know about some data structures.
Earlier, programmers had to use multiple variables to store related data, which make the code more difficult to write, read and maintain. This also made it more difficult to perform mathematical operations on data such as sorting or searching.
Arrays was introduced in 1945 to solve these problems by allowing the programmers to store multiple values under a single variable name, and it provided the indexing system which made it easy to access and manipulate individual elements of the array. They also provided a way to improve the performance of the program in terms of memory usage.
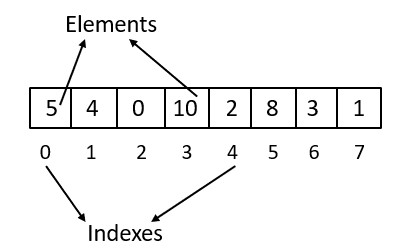
So, arrays are data structures that stores a collection of elements of any data type in a continuous memory space.
Some basic operations which we can do in an array are: accessing an element, traversing the array, searching an element, insertion of an element deletion of an element, sorting, reversing the array etc.
Real world applications of arrays:
The need for matrices arose from the requirement to efficiently store and manipulate large collections of data that have a two-dimensional structure.
For example, a matrix can be used to represent a table of numbers, where each row represents a different record and each column represents a different field.
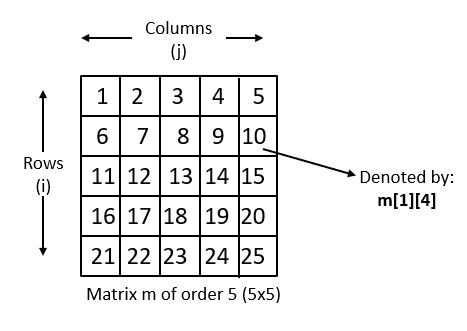
Matrix is a two dimensional array of elements, usually numbers or expressions. Each cell of a matrix is denoted by its row and column indices, and each of these cells are accessed using this notation matrix[row][column] . Matrices are also known as a two-dimensional arrays, tables or grids.
The different operations carried out in a matrix are: matrix addition, subtraction, scalar multiplication, matrix multiplication, transpose, determinant; inverse, trace, eigenvalues and eigenvectors.
Real world applications of matrix:
Arrays are powerful data structure that can be used to store and manipulate large sets of data, but it still have some limitations when it comes to certain things.
One main limitation is that they do not have any built-in mathematical operations defined for them. This makes it more difficult to perform mathematical operations on arrays. Another limitation is that they do not have a clear geometric interpretation. They do not have any built-in concepts such as length, angle or direction, which are important for representing geometric objects. Also a vectors size is not fixed whereas an arrays size is.
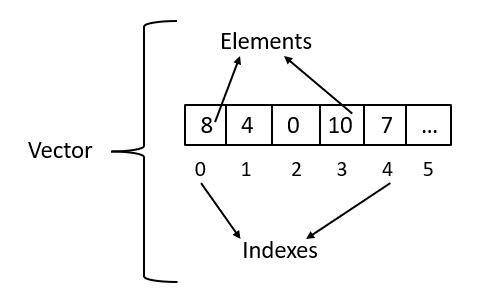
Hence vectors! A vector is a one-dimensional array of elements, usually numbers, symbols or expressions. Vectors are similar to arrays in that they store a collection of elements. Vectors are specifically designed to represent mathematical objects that have mathematical operations defined for them, such as addition, subtraction, and scalar multiplication. This makes it much simpler to perform mathematical operations on vectors.
On top of that vectors have a clear geometric interpretation as they have a direction and a magnitude. This makes it easy to reason about the properties of the vectors in space, such as the distance between two vectors, or the angle between two vectors etc.
Some common operations in a vector are: Vector addition and subtraction, scalar multiplication, dot product, cross product, magnitude, projection etc.
Some real-world applications are:
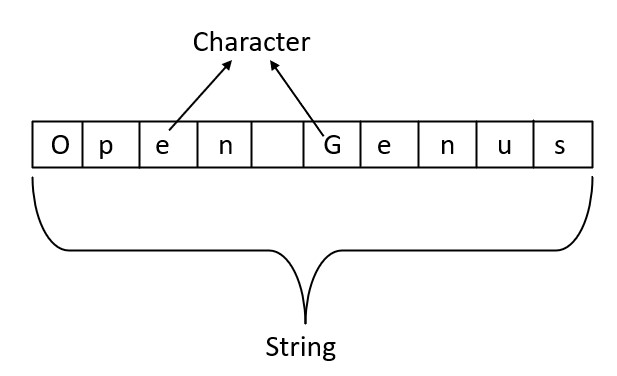
The need for strings arose from the requirement to efficiently represent and manipulate text data in computer programs. With the development of computer and the rise of the internet, the need for storing and manipulating text data has become increasingly important. With the use of text, human-computer interaction became more natural, which made it easier to use computers for a wide range of tasks, from writing and editing documents, to sending and receiving emails, to searching the web. Strings provide a way to store and manipulate text data in a concise and efficient way. A string is a sequence of characters, such as letters, numbers, symbols, or spaces, that can be stored and manipulated as a single entity.
Some operations in strings are: concatenation, scanning, comparison, slicing, encoding/decoding, sub-stringing, translation and verification.
Some real-world applications are:
Arrays, which are a common data structure for storing and manipulating data, have a fixed size and cannot be easily resized. This makes it difficult to efficiently store and manipulate dynamic sets of data. Hence the need for a way to effectively store and manipulate dynamic sets of data arose.
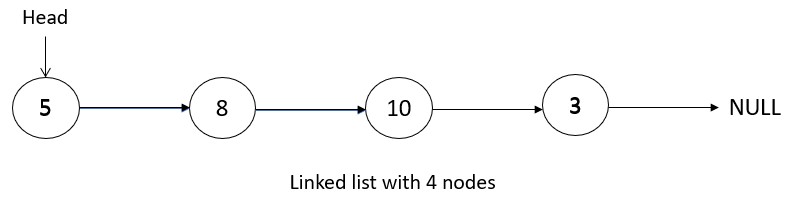
A linked list is a data structure that consists of a sequence of elements, called nodes, where each node contains a reference (or "link") to the next node in the list. Linked lists are a powerful data structure that can be used to store and manipulate large sets of data.
These linked list are dynamic data structures that can be easily resized as needed. This makes linked lists well-suited for storing and manipulating dynamic sets of data, such as in applications where elements are frequently added or removed from the list, which are difficult in arrays. Some common operations in a linked lists are: Insertion, deletion, traversal, searching, sorting, counting etc.
Some real-world applications are:
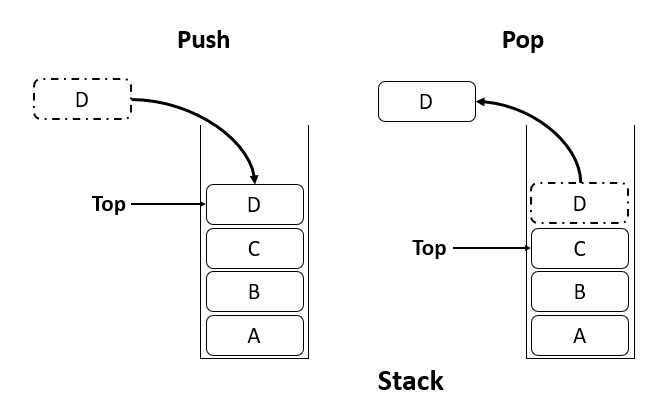
There was no way to efficiently store and manipulate elements in a specific order, such as a situation where elements need to be added and removed in a specific order, and the most recently added element is the first one to be removed. Hence the need for stacks arose.
A stack is a linear data structure that follows the Last In First Out (LIFO) principle. This means that elements are added and removed from the same end, called the "top" of the stack. When an element is added to the stack, it is said to be "pushed" onto the stack, and when an element is removed from the stack, it is said to be "popped" off of the stack.
Some common operations in a stack are: Push, pop, peek, isEmpty, size etc.
Some real-world applications are:
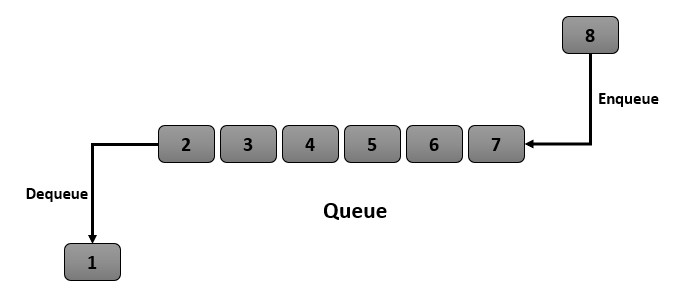
There came a situation where we needed to store and manipulate data in such a way that the oldest element is the first one to be removed. This was the way how, need for queue data structure arose. A queue is a linear data structure that follows the First In First Out (FIFO) principle, where elements are added to the back of the queue and removed from the front of the queue. The common operations are enqueue, dequeue, peek, isEmpty, size, clear.
Some real-world applications are:
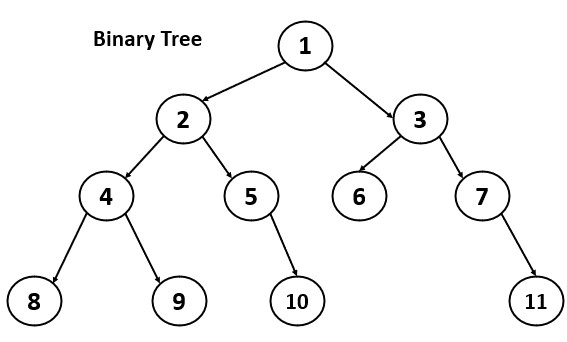
We needed to efficiently store and manipulate hierarchical data, where each item has a parent-child relationship with other items, for this purpose binary tree was introduced. Its a data structure composed of nodes where each node has at most two child nodes.
Some common operations are: insertion, deletion, searching, traversal etc.
Some real-world applications are:
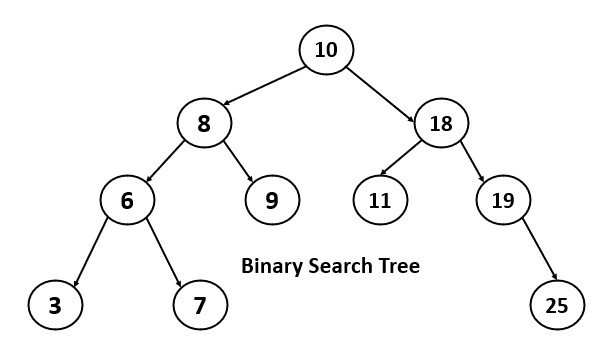
The need for binary search trees arose from the requirement to efficiently store and search for data in a way that allows for fast search times.
A binary search tree (BST) is a type of binary tree that is specifically designed to efficiently store and retrieve data. The main advantage of a BST is its ability to perform fast searches. Because the tree is organized such that all the values in the left subtree of a node are less than its value, and all the values in the right subtree are greater than its value.
Some common operations are: Insertion, deletion, searching, traversal, clone a tree, serialize and de-serialize etc.
Some real world applications are:
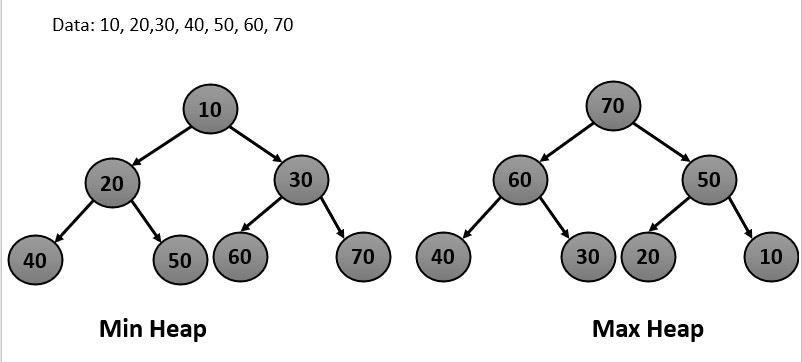
The need for heap arises from the requirement to efficiently store and retrieve data in a way that allows for fast access to maximum or minimum element. A heap is a specialized tree-based data structure that is used to efficiently implement priority queues. In a max heap value of each node is greater than or equal to the values of its children and vice versa in min heap.
Some common operations are: Accessing min or max element, insertion, deletion, heapifying etc.
Some real-world applications:
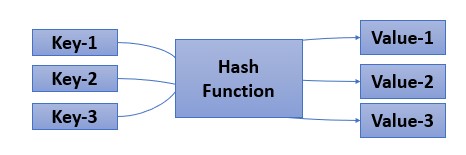
We needed a way to efficiently store and retrieve data in a way that allows for fast access to specific elements, and this way hashing was introduced. It is a method of mapping data of any size to a fixed size, called a hash value using a mathematical function called hash function.
Some operations are: insertion, deletion and searching.
Some real-world applications:
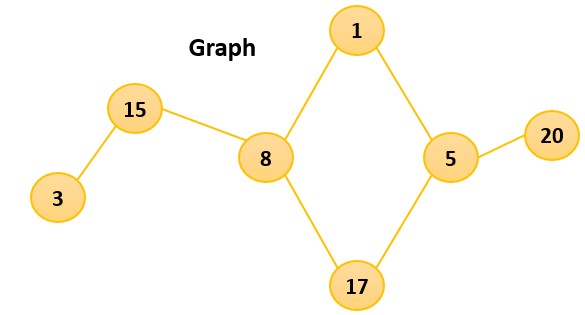
Graphs came to existence to tackle the problem of representing and modeling relationships between objects or entities. Graphs are a collection of vertices and edges, which connect the vertices. The vertices represent the objects or entities and the edges represent the relationship between them.
Some operations are: Adding and removing a vertex or edge,searching, shortest path, etc.
Some real-world applications are:
The need for suffix arrays arises from the requirement to efficiently search for patterns within a large text. A suffix array is a compact data structure that allows for efficient search for patterns within a large text. It is an array of all the possible suffixes of a given string, sorted lexicographically.
Some common operations are: construction, searching, longest common prefix, counting distinct substrings etc.
Some real world applications are:

The need for trie arises from the requirement to effectively store and search for strings, where prefixes of the strings are also important. A trie (also called prefix tree), is a tree like data structure which can be used to store a collection of strings. Each node represents a character in a string, and the path from the root node to that node represents the a string in the collection.
Some common operations are: insertion, deletion, searching, prefix search, counting words, auto-complete etc.
Some real world applications are:
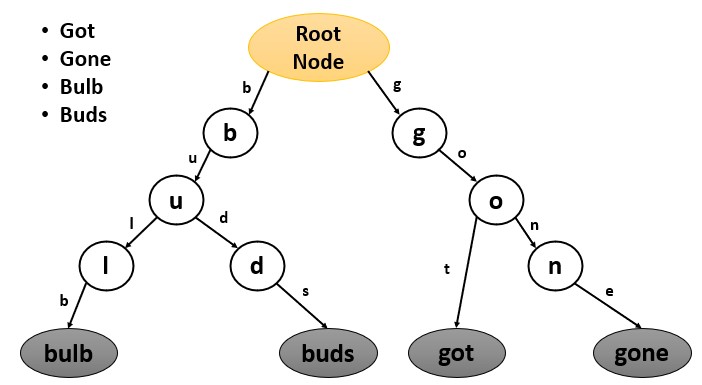
We can use trie data structure for operations on strings, but when it came to storing multi-dimensional data such as points or rectangles in a 2D space we had no option to do that. This was why x/y trie data structure was introduced.
In x/y-trie, the root of the trie is the origin of the 2D space and each level in the trie corresponds to a different dimension. Each internal node of the trie is a split point, and the edges leaving the node represent the two subregions separated by the split point.
Some operations in x/y trie: insertion, searching, deletion, range queries, point location, nearest-neighbor point etc.
Some real-world applications are:
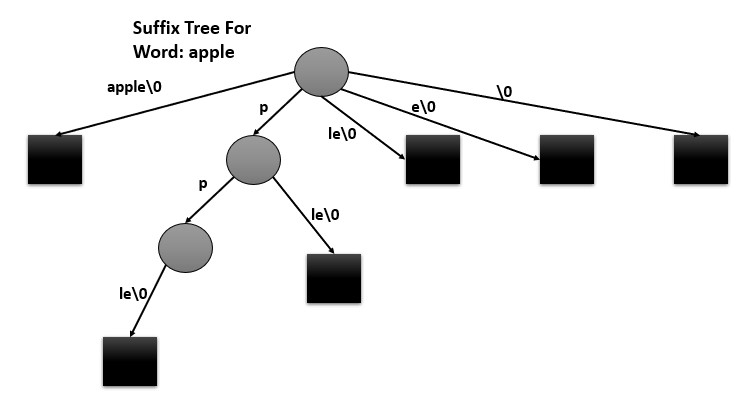
The need for a suffix tree arises from the requirement to efficiently search for patterns within a large text. A suffix tree is a data structure that is used to store all the possible suffixes of a given text, and it allows for efficient search for patterns within the text, with a time complexity of O(m) for searching, where m is the length of the pattern. A suffix tree is a compressed trie of all the suffixes of a given string. It is a space-efficient alternative to suffix arrays.
Some operations includes: construction, searching, longest repeated substring etc.
Some real-world applications are:
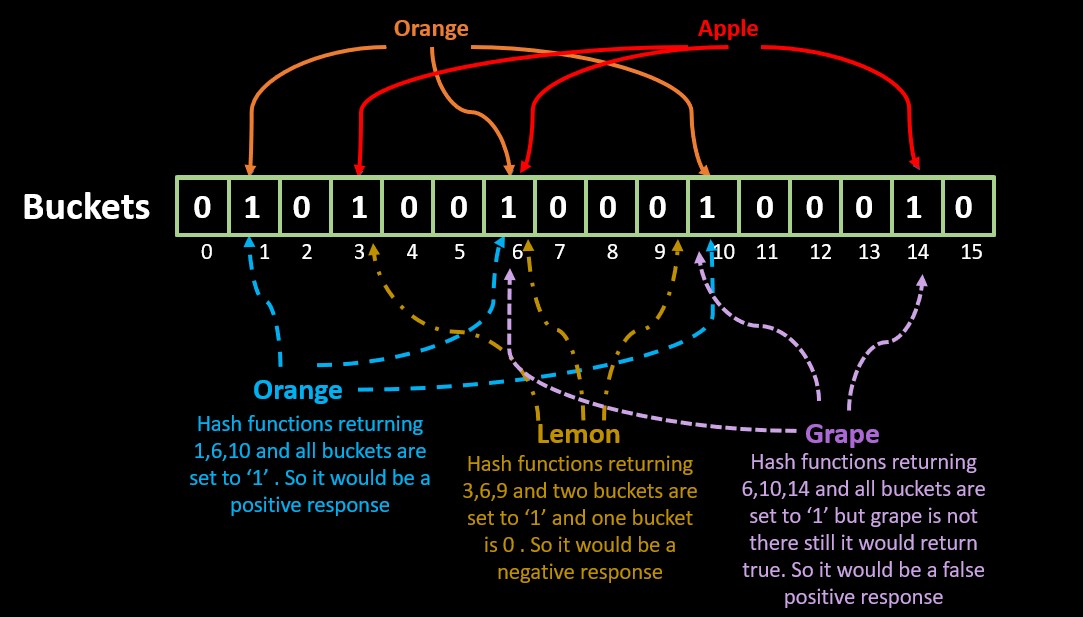
The need for a Bloom filter arises from the requirement to efficiently check if an element is a member of a set or not, when the set is too large to be stored in the memory. A Bloom filter is a probabilistic data structure that is used to test whether an element is a member of a set or not. It is a space-efficient data structure that uses a small amount of memory to store the set, but at the cost of a small probability of false positives (i.e., incorrectly reporting that an element is in the set when it is not).
Some common operations are: insertion, deletion member test.
Some real-world applications are:
The need for a B-tree arises from the requirement to efficiently store and search large amounts of ordered data that doesn't fit in memory. B-tree is a self-balancing tree data structure that keeps data sorted and allows search, sequential access, insertion, and deletion operations with logarithmic time complexity.
Common operations are: insertion, searching, deletion, range queries, traversal etc.
Some real-world applications:
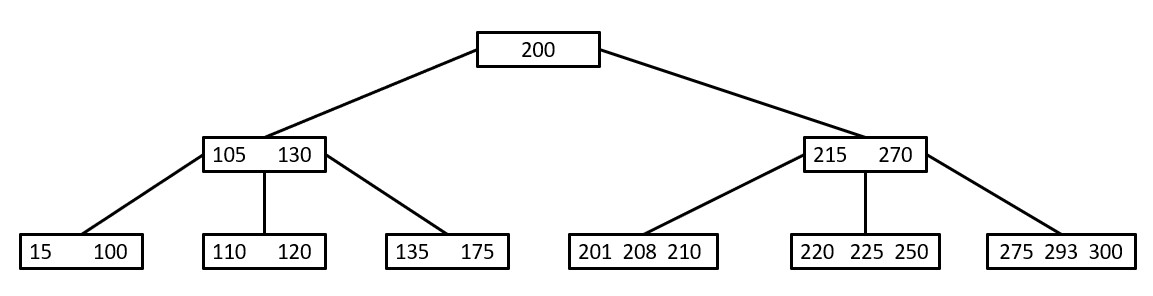
If you want to learn about B+ Trees and about its complexities click here.
If you want to learn about (a,b) trees click here.
The need for a Segment Tree arises from the requirement to efficiently perform operations such as range queries, range updates, and range minimum/maximum on an array of data. A Segment Tree is a data structure that can be used to perform these operations on an array in logarithmic time complexity. A segment tree represents a given array as a binary tree, where each leaf node represents an element of the array and each internal node represents a range of elements in the array.
Some common operations are: range query, range update, point update etc.
Some real-world applications:
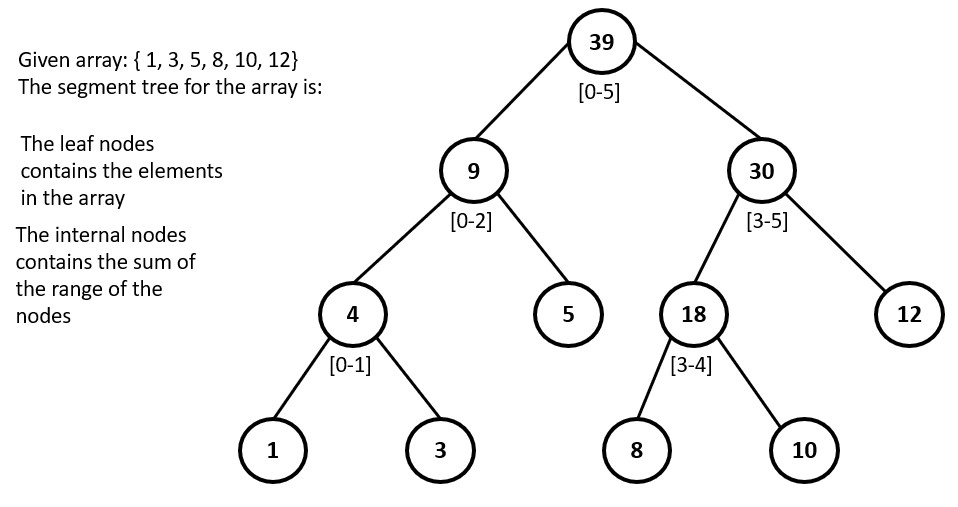
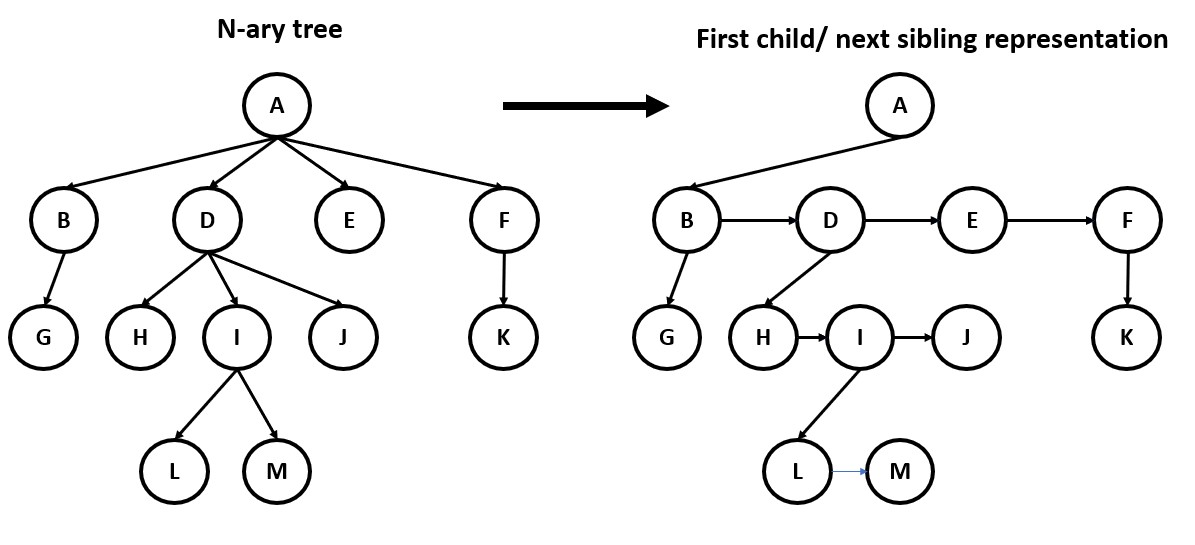
The need for a n-ary tree (Generic Tree) arises from the requirement to efficiently store and search hierarchical data structures where each node can have more than two children. An n-ary tree is a tree data structure where each node can have an arbitrary number of children, rather than the binary tree structure where each node can have at most two children.
Some common operations are: Insertion, traversal searching and deletion.
Some real-world applications are:
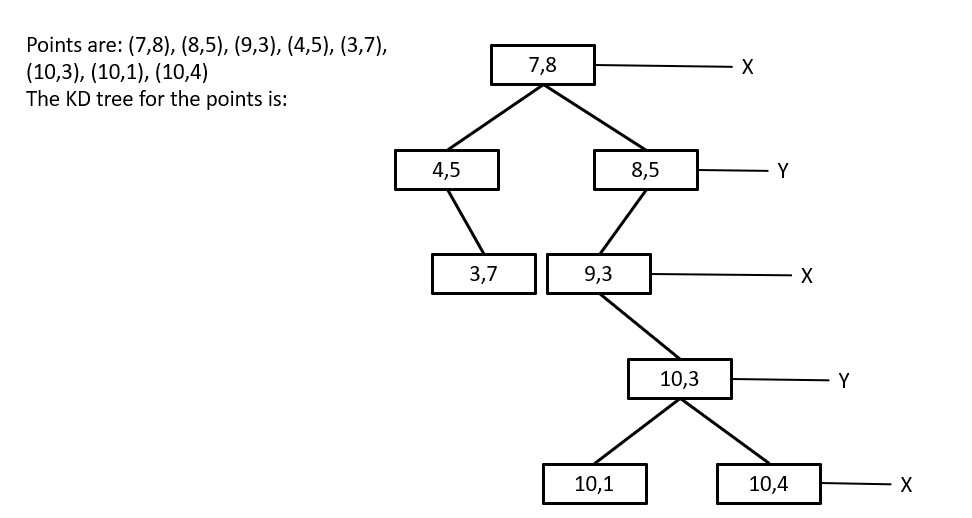
The need for a k-dimensional tree arises from the requirement to efficiently perform operations such as search, nearest neighbor search, and range search on large multi-dimensional data sets.
A k-dimensional tree is a type of space-partitioning data structure used to organize points in a k-dimensional space. It is a generalization of a binary search tree, where each internal node in the tree represents a split in k-dimensional space, rather than just a split in one dimension as in a binary search tree.
Some common operations are: Insertion, searching, nearest neighbour search, range search etc.
Some real-world applications:
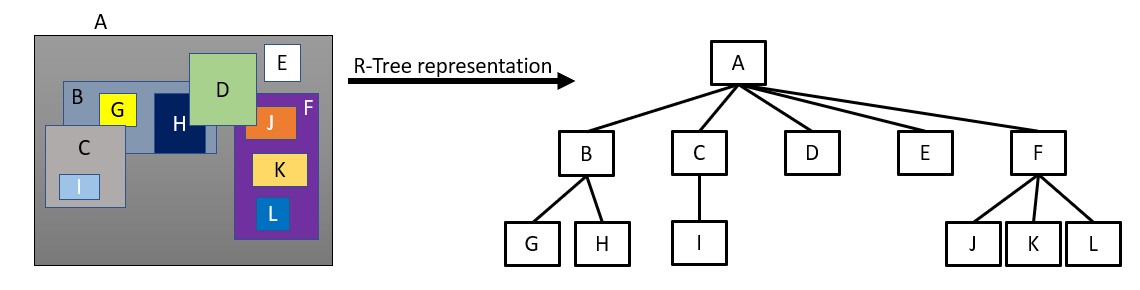
The need for an R-tree arises from the requirement to efficiently store and search large amounts of multidimensional spatial data, such as geographic coordinates or geometric shapes. An R-tree is a type of spatial indexing data structure that organizes data in a hierarchical tree structure based on their spatial relationships.
Some common operations are: insertion, deletion, searching, building, re-balancing.
Some real-world applications are:
The need for a Count Min Sketch arises from the requirement to estimate the frequency of elements in a large stream of data, such as a data feed or a log file, with a high degree of accuracy. Count Min Sketch is a probabilistic data structure that provides approximate answers to questions about the frequency of elements in a stream, using a small amount of memory. It is a useful data structure when it is impractical to keep an explicit count of all the elements in a stream, due to the large number of distinct elements or the high rate of incoming data.
Some common operations are: insertion, query, update, building etc.
Some real-world applications are:
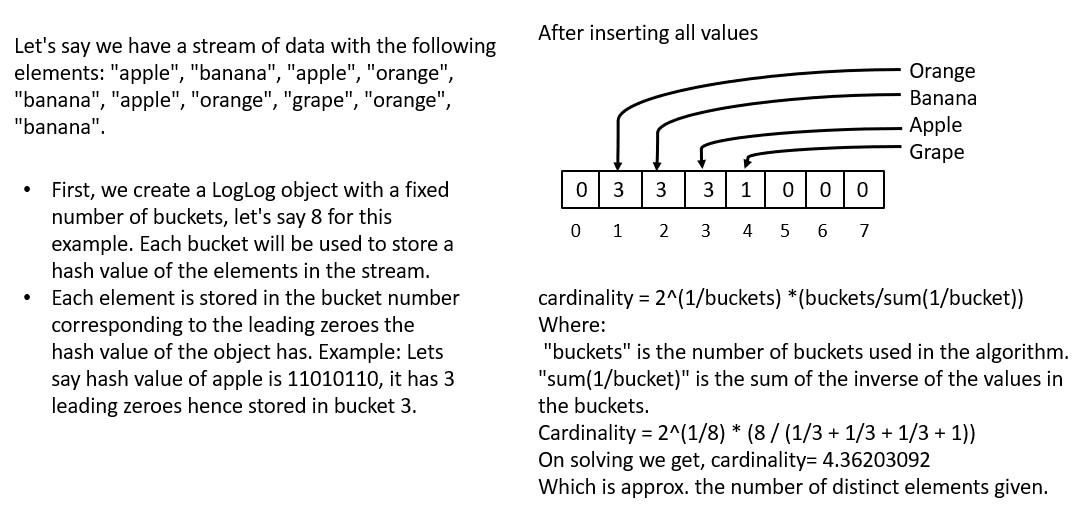
The need for a LogLog algorithm arises from the requirement to estimate the number of distinct elements in a large stream of data, known as the "cardinality" of the set. LogLog is a probabilistic algorithm that uses a small amount of memory to estimate the cardinality of a set with a high degree of accuracy. It is particularly useful when the exact number of distinct elements is not needed, but only an approximation of it is required, or when the data is too large to store in memory.
Some common operation: insertion, cardinality, building.
Some real-world application:
Now you have reached the end of this article. Now you will be having the knowledge of different data structures, why it was introduced, different operations, real-world applications and its representation.
Aswin Shailajan is a B. Tech Computer Science student at Vellore Institute of Technology and is a SDE, Intern at OpenGenus.
Improved & Reviewed by:
OpenGenus Tech Review Team
— OpenGenus IQ: Learn Algorithms, DL, System Design —In this article, we will understand how casting operates on the CPU level in C Programming Language along with the concept of zero-extension and sign-extension. This is a core concept in C Programming and Embedded Programming.

Benjamin QoChuk, PhD
B+ trees an interesting name isn't it? So in this article, we will closely analyze the time & space complexities for different operations in different cases of B+ Tree Data Structure.